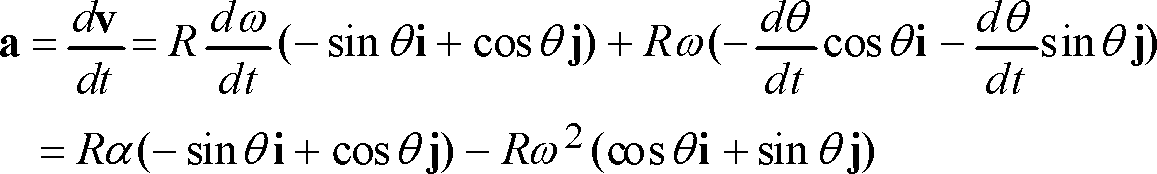Time Period Of A Satellite Derivation

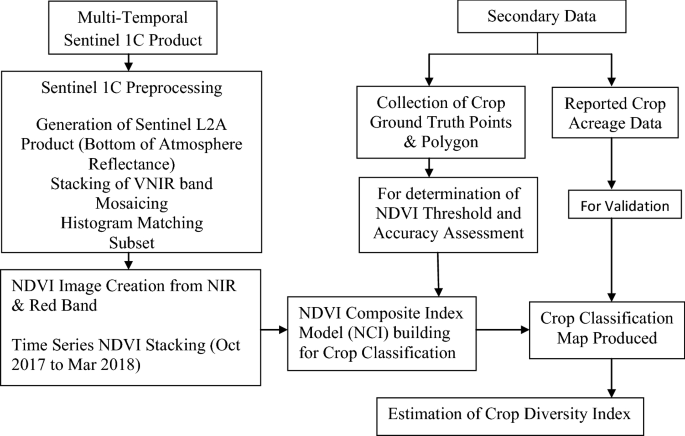
Here m is the mass of earth and m is the mass of the satellite which is having a uniform circular motion in a circular track of radius r around the earth.

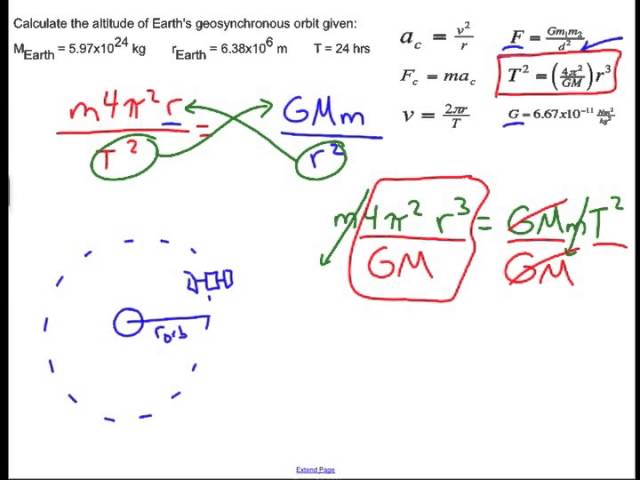
Time period of a satellite derivation. Say period of revolution is t and the radius of the orbit is r. Artificial satellites are of two types. V is the linear velocity of the satellite at a point on its circular track. The period of the earth as it travels around the sun is one year.

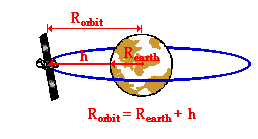
Doppler effect the observer will measure the moving clock as. R r h radius of the earth hight of the satellite from the surface of the earth. The period of a satellite is the time it takes it to make one full orbit around an object. Say period of revolution is the and the radius of the orbit is r.

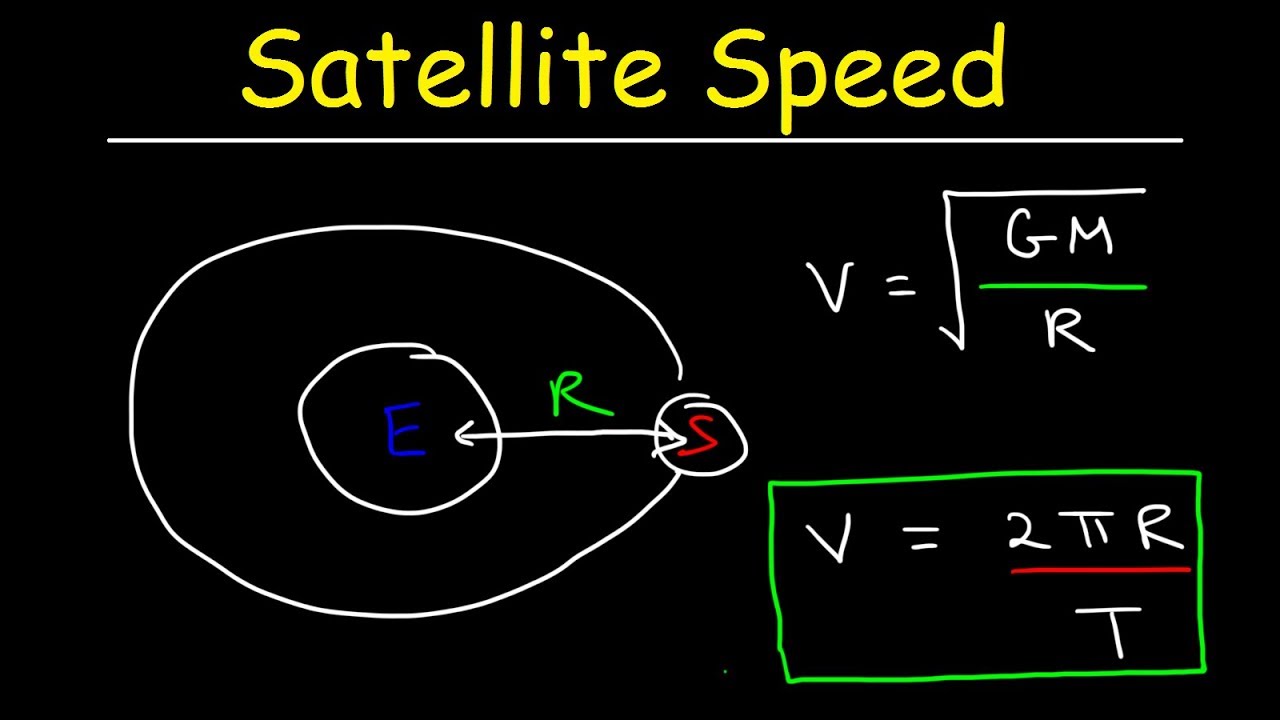
Time period of revolution of earth satellite. Binding energy of satellite definition. Orbital velocity is derived in the following way. And r r h radius of the earth height of the satellite from the surface of the earth.

If the injection velocity is less than the calculated value the satellite will fall back to the earth. If you know the satellite s speed and the radius at which it orbits you can figure out its period. Mass of the earth. Time period of revolution of the satellite about the earth and kepler s third law derivation.

T 2π r g 5 08 10 3 s 84 min. Need help understanding the derivation of hydrostatic equilibrium in a star 0 if the orbital period of a smaller body is longer why does the moon not fall behind the earth in their orbit around the sun. You can calculate the speed of a satellite around an object using the equation. The energy required by a satellite to leave its orbit around the earth planet and escape to infinity is called binding energy of the satellite.

Please mark me as a brainlist answer. Geostationary or parking satellites. F g frac gmm r 2 gravitational force between the earth and the satellite eq 1 f c frac mv 2 r centripetal force acting upon the satellite eq 2 where m. Binding energy of the satellite of mass m is given by.

After compensating for varying signal delays due to the changing distance between an observer and a moving clock i e. So period of revolution t 2 π r v. Time period of a satellite. Time period of revolution of the satellite about the earth and kepler s third law derivation.

T 2π r 3 gm 2π r h 3 g g gm r 2. Mass of the satellite. Where p is the average density of earth. By knowing the value of time period the height of the satellite from the earth surface can be calculated.

Time dilation is a difference in the elapsed time measured by two clocks either due to them having a velocity relative to each other or by there being a gravitational potential difference between their locations. T 2π r 3 gm 3π gp. Time taken by the satellite to complete one revolution round the earth is called time period. Derivation of orbital velocity.

T 2πr v 0 2π r h v 0. Near the earth surface time period of the satellite.